ATRACTOR

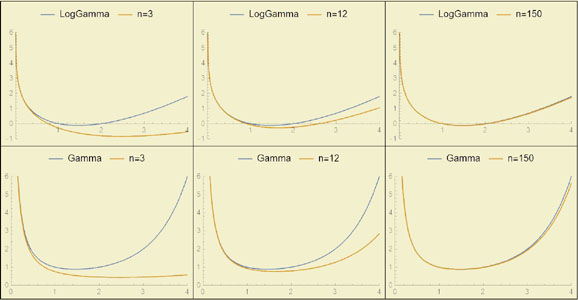
Figura 4

A propriedade (1) permite calcular a função $\Gamma$ se se conhecerem os valores que toma em $]0,1]$, uma vez que (1) implica que

(3) $\Gamma(x + n) = (x + n - 1) \cdots (x+1)\,x\,\Gamma(x) \quad \quad \forall\, 0 < x \leqslant 1 \quad \forall\, n \in \mathbb{N}.$

Mas impede que a possamos estender de modo contínuo a $0$, pois obteríamos $\Gamma(1) = 1 = 0 \times \Gamma(0) = 0$. Admite, todavia, um prolongamento a $\mathbb{R}^- \setminus \mathbb{Z}^-$, e essa extensão, além de continuar a verificar (1), tem a seguinte relação com a função seno $$\Gamma(x)\, \Gamma(1-x) = \frac{\pi}{\text{sen}\,(\pi\,x)} \quad \quad \forall\, x \notin \mathbb{Z}$$ que é útil para o cálculo de imagens de $\Gamma$. Por exemplo, dela resulta que $\Gamma(1/2) = \sqrt{\pi}$ logo, usando (1), que $\Gamma(3/2)=\frac{1}{2}\,\Gamma(1/2) = \sqrt{\pi}/2.$ A figura 5 mostra um esboço do gráfico de $\Gamma$ e da sua intersecção com a linha recta de equação $y=x$ (a tracejado).

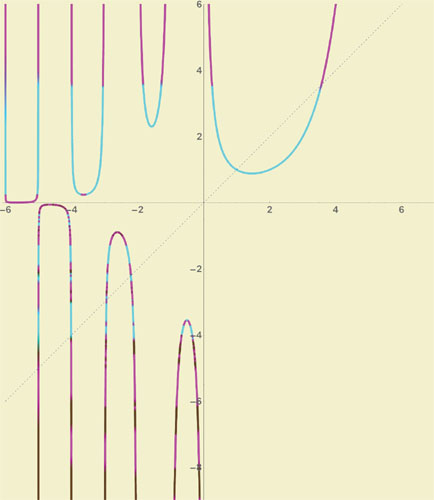
Figura 5

Página seguinte